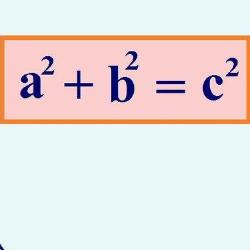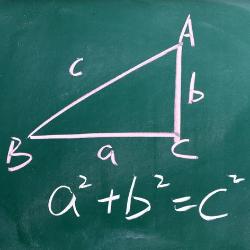-
Данный тест состоит из 15 вопросов различной вариативности, от теоретических вопросов до решения задач и уровня сложности от простого до сложного, некоторые вопросы включены из сборника ОГЭ!
-
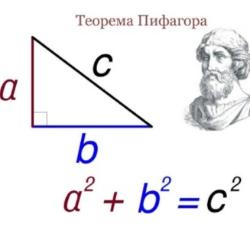
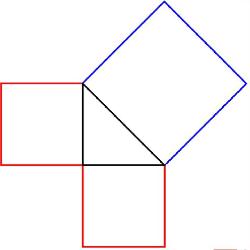
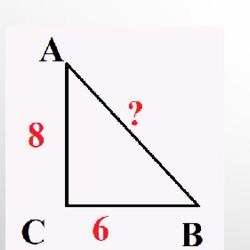
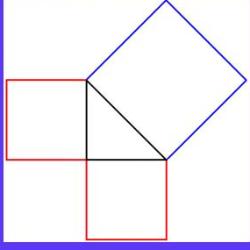
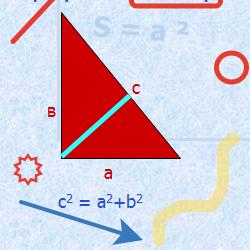
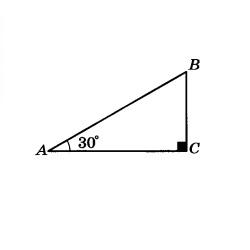
Тест содержит 7 вопросов по геометрии,тема теорема Пифагора, предназначен для учеников 8 класса. В тесте 2 задания с выбором ответа и 5 заданий с вводом числового ответа. Тест содержит простые задачи на умение находить гипотенузу и катет прямоугольного треугольника,по известным 2 сторонам. В нем есть более сложные задачи с использованием теоремы Пифагора и других формул и теорем геометрии, например, формул площадей и периметра геометрических фигур. В заданиях кроме прямоугольного треугольника надо знать и уметь применять свойства равнобедренного треугольника, прямоугольника, ромба. Вычислять площадь прямоугольника, прямоугольного треугольника, ромба. Уметь вычислять площадь ромба через диагонали.
-
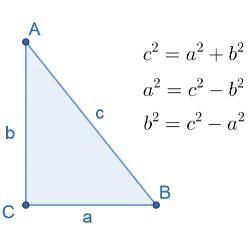
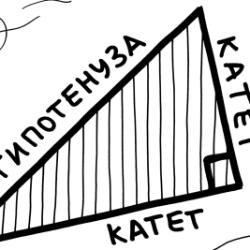
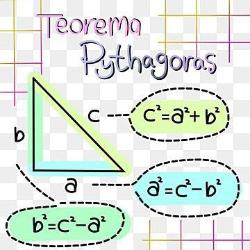
Онлайн тест за закрепление теоремы Пифагора. Геометрия 8 класс.
-
Работа состоит из 11 заданий. Есть тестовые задания и задачи, где нужно вписать только ответ (число).
-
Тест предназначен для учащихся 10 классов для проверки уровня усвоения материала по теме "Теорема о трёх перпендикулярах". Для того, чтобы решить задачи теста и ответить на вопросы, необходимо повторить понятия наклонной и перпендикуляра к плоскости, формулировку теоремы о трёх перпендикулярах, теорему Пифагора и свойства параллелограммов.
-
Контрольная работа содержит 6 вопросов; из которых часть с выбором вариантов ответа и часть с вводом правильного ответа
-
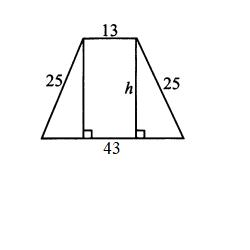
Тест проверяет не только вычислительные навыки, но и понимание условия применения теоремы, умение строить логические рассуждения и применять теорему в нестандартных ситуациях (равносторонний треугольник, трапеция, свойства высоты).
-
Тест предназначен для учащихся 8 или 9 класса средней школы для проверки уровня знаний по теме "Пропорциональные отрезки в прямоугольных треугольниках."
-
Тест по геометрии по теме "Теорема Пифагора" 8 класс по учебнику Погорелова
-
Решите задачи по теме "Теорема пифагора". Если возникли вопросы, подойдите ко мне.
-
Тест предназначен для подготовки к ОГЭ по темам: теорема Пифагора, средняя линия треугольника, тригонометрия.
-
Геометрия. Теорема Пифагора. Тест по теме «Теорема Пифагора». Вариант № 5
-
Домашнее задание в тестовой форме. В тесте 5 вопросов. Система оценивания: "5" - 5 верно выполненных заданий (95%) "4" - 4 верно выполненных заданий (75%) "3" - 3 верно выполненных заданий (55%) "2" - 2 и менее верно выполненных заданий (меньше 55%)
-
Тест предназначен для учащихся 8 класса по геометрии при изучении теоремы Пифагора.
-
Геометрия. Теорема Пифагора. Тест по теме «Теорема Пифагора». Вариант № 10
-
Тест для диагностики знаний по теме "Пропорциональные отрезки в прямоугольном треугольнике"
-
Тест для диагностики знаний по теме "Пропорциональные отрезки в прямоугольном треугольнике"
-
Тест по темам: "Соотношения в прямоугольном треугольника. Теорема Пифагора" для обучающихся в 8 классе.
-
Ребята, данный тест нацелен на то, чтобы определить степень усвоения новой темы. (Сложность: лёгкий)
-
Тест по геометрии 8 класс по учебнику Погорелов по закреплению теорема Пифагора
-
тест по геометрии 8 класс , учебник Погорелов , по теме : Теорема Пифагора
-
Домашнее задание в тестовой форме. В тесте 5 вопросов. Тест содержит простые задачи на умение находить гипотенузу и катет прямоугольного треугольника.
-
Тест для обучающихся 8 класса Теорема Пифагора____________________
-
Тест по теме "Теорема Пифагора, метрические соотношения" для проверки своих знаний.
-
Данный тест предназначен для 8 класса. Тест проверяет знания теоремы Пифагора
-
Тест по геометрии для обучающихся 8 класса по теме "Терема Пифагора"
-
Геометрия. Теорема Пифагора. Тест по теме «Теорема Пифагора». Вариант № 1
-
Геометрия. Теорема Пифагора. Тест по теме «Теорема Пифагора». Вариант № 2
-
Геометрия. Теорема Пифагора. Тест по теме «Теорема Пифагора». Вариант № 3
-
Геометрия. Теорема Пифагора. Тест по теме «Теорема Пифагора». Вариант № 4
-
Геометрия. Теорема Пифагора. Тест по теме «Теорема Пифагора». Вариант № 6
-
Геометрия. Теорема Пифагора. Тест по теме «Теорема Пифагора». Вариант № 7
-
Геометрия. Теорема Пифагора. Тест по теме «Теорема Пифагора». Вариант № 8
-
Геометрия. Теорема Пифагора. Тест по теме «Теорема Пифагора». Вариант № 9
-
Геометрия. Теорема Пифагора. Тест по теме «Теорема Пифагора». Вариант № 11
-
Геометрия. Теорема Пифагора. Тест по теме «Теорема Пифагора». Вариант № 12
-
Тест для диагностики знаний по теме "Пропорциональные отрезки в прямоугольном треугольнике"
-
Тест по математике разработан для учащихся 5 класса, которые обучаются по учебнику В. В. Козлова. Для закрепления и проверки знаний по теме: "Теорема Пифагора", "Вычисление сторон прямоугольного треугольника"
-
Тест, блок геометрии ОГЭ. Разноуровневые задания, с различными комбинциями при выборе ответов.
-
тест по геометрии по программе Погорелова по теме теорема Пифагора
-
Тест включает в себя 19 заданий. Из них первые 16 заданий с одиночным выбором ответа, остальные 3 с введением числа. 9 заданий на знание теории, 10 практических.
-
Тест на проверку усвоения теоремы Пифагора и теоремы, обратной теореме Пифагора.
-
Тест предназначен для проверки знаний учащихся 8 класса по теме: "Теорема Пифагора"
-
Проверьте свои знания понятий синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике
-
Тест состоит из 5 вопросов. Тип вопросов: открытый; с выбором ответа; с множественным выбором ответа.
-
Тест для обучающихся 8 класса по геометрии. Тема: "Теорема Пифагора"
-
Тест для обучающихся 8 - го класса по геометрии. Тема: "Теорема Пифагора"
-
Обазовательный тест по теме "Прямоугольный треугольник" Геометрия 8 класс
-
В тесте предложено 10 вопросов различного типа. В заданиях где требуется вычислить значения, единицы измерения в ответ вность не нудно, ответ должен быть числом. Выбор последовательности слов или букв можно осуществлять с помощью мыши, перетаскиванием.
-
Данный тест рекомендуется проходить ученикам 7-9 класс, чтобы усвоить и закрепить полученные навыки по теме "Теорема Пифагора". Данный тест включает в себя разнообразные вопросы: с выбором ответа, с соединениями, с вписанием слова, с введением числа в строку. Такой формат не только поможет ученику освоить материал, но и даст возможность провести увлекательно время урока. Сложность вопросов: лёгкая.
-
Тест предназначен для проверки знаний учащихся 8 класса по теме: "Теорема Пифагора"
-
Тест содержит 7 вопросов по геометрии,тема теорема Пифагора, предназначен для учеников 8 класса. В тесте 2 задания с выбором ответа и 5 заданий с вводом числового ответа. Тест содержит простые задачи на умение находить гипотенузу и катет прямоугольного треугольника,по известным 2 сторонам. В нем есть более сложные задачи с использованием теоремы Пифагора и других формул и теорем геометрии, например, формул площадей и периметра геометрических фигур. В заданиях кроме прямоугольного треугольника надо знать и уметь применять свойства равнобедренного треугольника, прямоугольника, ромба. Вычислять площадь прямоугольника, прямоугольного треугольника, ромба. Уметь вычислять площадь ромба через диагонали.
-
Все задания взяты из сборника Маракулина. Данный вид задания вы можете решить с помощью формул из справочных материалов или создать собственные размышления и прийти к верному ответу.